(총평)
확통 되게 잘냈다. 특히 27번
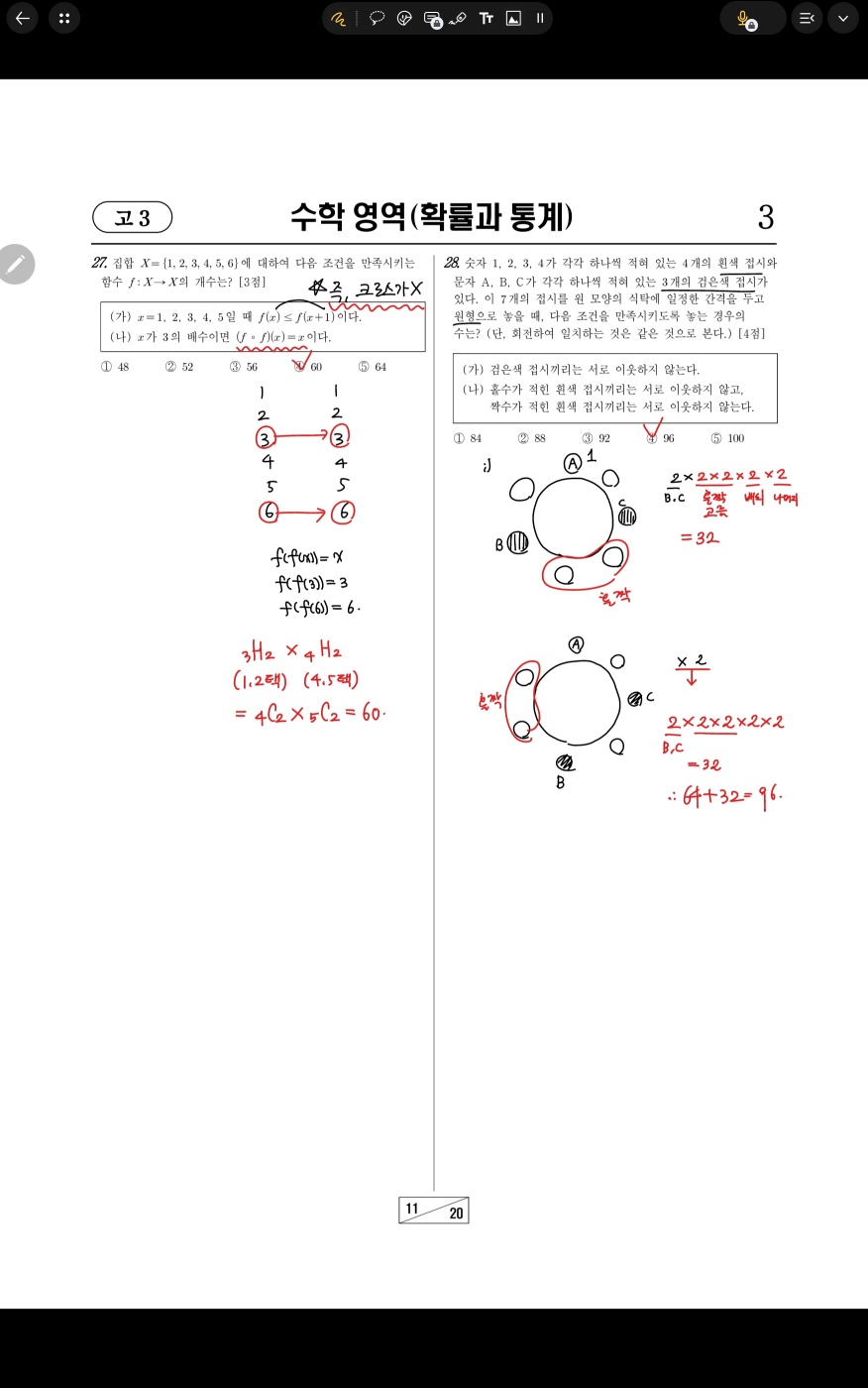
#27
(가)조건에서 f는 약증가한다. 아마 중복조합 문젠가보다.
(나)조건에서 f(f(x))=x이므로... 이 경우 f(x)=x or f(a)=b, f(b)=a (cross)를 만족한다.
그런데!! (가)조건에 의해, f는 증가만하므로, 교차 케이스는 발생하지 않는다.
따라서 f(3)=3, f(6)=6이다. 이후엔 나머지 정의역만 정해주면 된다.
#28
A를 고정시킨다.(X1) 이제 B,C 자리를 정해주는건 3가지다. 경우를 나눠서 앉히면,
어떤 경우든지 흰색 접시는 홀로 2개, 이웃하여 1쌍 이런 형태로 남는다.
따라서 이웃한 쌍엔 홀짝을 넣어주고, 나머지 자리도 결정해주면 된다.
한번에 풀면 3(B,C자리)*2(B,C배치)*2*2*2(이웃할 홀짝선택후 배치)*2(나머지2개배치)=96
#29
짝수를 1개 이하로 택하면 16의 배수가 될 수 없다. 따라서 짝수개수는 2,3,4개인 경우로 나누어 계산하면 된다.
#30
ABC + DE = 8인데, ABC가 홀수이므로... DE도 홀수다. 그리고 D=2E이므로, (D,E)=(2,1)이다.
E=1이므로 WLOG 검은색 1개로 배치하고 2를 곱한다.
이제 (D검, D흰)=(2,0), (1,1), (0,2)인 경우로 나눠 중복조합 계산을 열심히 해주면 된다.

'취미 > 수학' 카테고리의 다른 글
| 2025 3월 모의고사 기하 해설 (0) | 2025.03.28 |
|---|---|
| 2025 3월 모의고사 미적분 해설 (0) | 2025.03.28 |
| 2025 3월 모의고사 수학 공통 해설 (0) | 2025.03.28 |
| 재밌는 함수부등식 문제 (0) | 2025.02.25 |
| 2009 IMO P5 (함수방정식) (0) | 2025.01.31 |



댓글