1. 로지스틱 회귀란
로지스틱 회귀는 회귀식을 통해 사실 이진분류를 하는 방법입니다.
예를 들어 학생들의 영어, 수학, 국어 성적등(feature)과 시험합격여부 0, 1(label)이 주어지면,
회귀식을 통해 값 \(x\) 를 찾아내면 그 값으로 분류를 진행하는 것입니다.
통계학에서 두가지 결과만 있을 때, 이항분포의 일종인 베르누이 분포를 사용합니다.
확률론적 방법을 통해 특정 확률이상이면 분류를 시켜주는 방식으로 진행합니다.
우선, 이를 위해 실수값 \(x\) 를 확률 \(p\) 로 만들어주는 절차가 필요합니다.
2. 활성화 함수
활성화함수는 선형회귀식으로 얻은 함수를 곡선형태의 꼴로 변환시켜주는 역할을 합니다.
활성화함수가 되기 위한 조건으로는 미분시 자기자신으로 표현가능하거나, 값이 정의역에서 잘 정의되는등
좋은 역할들을 해야합니다. 이를 해주는게 대표적으로 sigmoid funcion(시그모이드 함수)입니다.
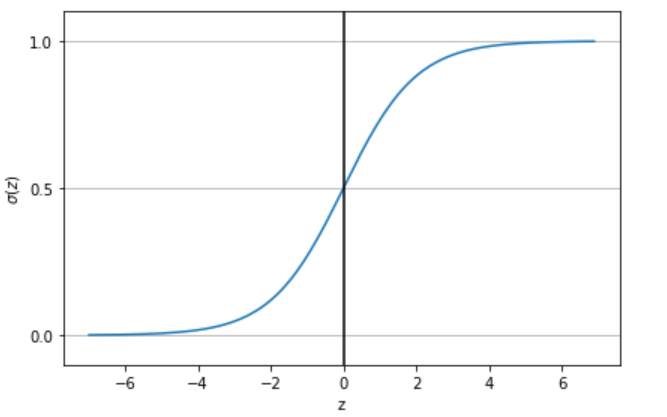
시그모이드 함수는 실수전체집합에서 0과 1 사이의 값을 갖는 대칭함수입니다.
$$ y=\frac{1}{1+e^{-x}} $$
시그모이드 함수를 거쳐 나온 값은 0과 1 사이 값을 갖는 확률값으로 변환됩니다.
또한 \(x=0\)을 기준으로 확률값이 0.5 가 나옵니다. 1 또는 0을 판단시, 활성화 함수의 최종결과가 0.5이상인지
아닌지에 따라 분류를 진행하는 경우가 많아 딱 적합함을 알 수 있습니다.
다른 활성화 함수로는 ReLU function( \(f(x)=max(0, x)\) )도 자주 쓰입니다.
3. 로지스틱 회귀 손실함수
로지스틱 회귀에서의 손실함수는 크로스 엔트로피 함수를 사용합니다.
$$ L=\sum (y_i{logp}+(1-y_i)log(1-p)) $$
이를 통해 경사하강법 \(w_i=w_i-\eta \frac{\partial L}{\partial w_i}\) 를 반복해주면 됩니다.
4. 로지스틱 회귀의 모식도
로지스틱 회귀의 진행순서를 나타낸 그림입니다.
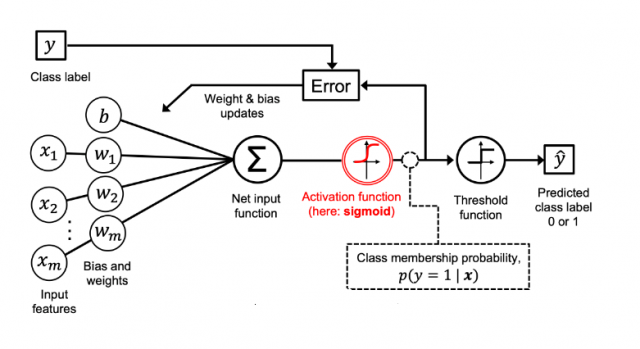
위 그림처럼 input feature \(x_i\)들이 주어졌을 때, \(w_1, w_2, ... , w_m\)을 찾아주는게 목적입니다.
\(w_i\)들을 초기설정 후, 값을 계산하고 활성화함수로 바꾸는 과정을 거칩니다. 이렇게 얻은 확률을 미리
설정한 확률 기준으로 나눠줍니다. 그럼 테스트 결과가 나오겠죠. 이걸 경사하강법으로 epoch번 수행하며
\(w_1, w_2, ... , w_m\) 을 조정해주면 됩니다.
'CS > 머신러닝' 카테고리의 다른 글
| 혼자 공부하는 머신러닝 + 딥러닝 - Ch2 (0) | 2023.01.07 |
|---|---|
| 혼자 공부하는 머신러닝 + 딥러닝 - Ch1 (0) | 2023.01.04 |
| 선형 회귀 - 경사 하강법 (0) | 2022.12.02 |
| 선형 회귀 - 최소제곱법 (0) | 2022.11.27 |
| 회귀와 분류 (0) | 2022.11.26 |


댓글