경사하강법(gradient descent)에 대해 정리해봅시다.
경사하강법은 이후 모델에서도 손실함수 MSE를 최적화하기 위한 방법으로
사용됩니다. 원리는 간단합니다. 경사하강법은 정확한 값을 한번에 구하는게 아니라
함수가 볼록하다는 점을 이용하여 계속해서 값을 업데이트해나가는 방식입니다.
즉, 경사하강법은 손실함수를 최소화하는 방향으로 파라미터를 업데이트하는 방식으로 작동합니다.

업데이트 방식은 학습률 \(\eta \) 에 대해,
$$w=w-\eta \frac{\partial L}{\partial w} , b=b-\eta \frac{\partial L}{\partial b} $$
를 반복해주면 됩니다.
미분방향의 역방향으로 갱신을 해줘야 볼록함수의 중앙으로 가게 되고, 거기에 학습률 곱해서
변화값의 증감을 조절해줄 수 있습니다. 이를 에폭(epoch)이라는 수를 미리 정해 이만큼까지
업데이트를 시켜주면 됩니다. 그럼 epoch은 미리 정하는 변수이니 하이퍼 파라미터가 되겠네요.
아래 코드는 sklearn의 학습용 데이터를 이용하여 경사 하강법을 구현한 것입니다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes
D=load_diabetes()
def gradient_descent(X, Y, epochs, lr):
# initial
w = 0.0
b = 0.0
# calculate dL/dw, dL/db
for i in range(epochs):
L = np.mean((Y-(w*X+b))**2) # MSE loss
dw = -2*np.mean(X*(Y-(w*X+b))) # dL/dw
db = -2*np.mean(Y-(w*X+b)) # dL/db
w -=dw*lr # w update
b -=db*lr # b update
return w,b
x=D.data[:, 2]
y=D.target
# find w,b
gradient_descent(x,y,1000,0.5)
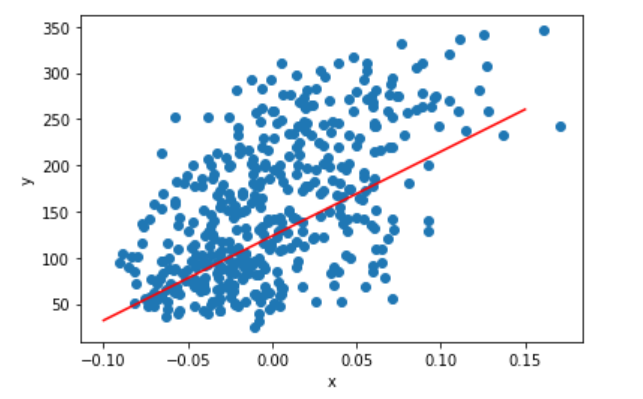
# draw graph
plt.scatter(x, y)
plt.plot([-0.10, 0.15], [-0.10*w+b, 0.15*w+b], color="red")
plt.xlabel('x')
plt.ylabel('y')
plt.show()
'CS > 머신러닝' 카테고리의 다른 글
| 혼자 공부하는 머신러닝 + 딥러닝 - Ch1 (0) | 2023.01.04 |
|---|---|
| 로지스틱 회귀 (0) | 2022.12.20 |
| 선형 회귀 - 최소제곱법 (0) | 2022.11.27 |
| 회귀와 분류 (0) | 2022.11.26 |
| 머신 러닝과 딥러닝 (0) | 2022.11.26 |

댓글